在学习新知识时，很多朋友往往总是想要急于求成，因此会忽略那些看似没有太大用处的基础知识，而基础知识的沉淀类似于盖房子的地基，房子能盖多高就取决于它。

前段时间的一个项目中，需要编写一个可以与某个设备进行长连接并接收数据的 TCP Server，该设备会把一些数据发送过来，让 TCP Server 进行解析。设备发送数据使用 C 语言开发，其中的数据中包括了浮点数。而 TCP Server 的开发并没有使用 C 语言或 C++ 进行，而是采用了 Java 语言的 Netty 框架进行开发，所以接收到的浮点数就需要进行转码。

最早开始接触 C 语言的时候，学习了 IEEE 浮点数表示的方式，后来也很少会接触到，更别提用到。但是，在这个项目中，当时学习的 IEEE 浮点编码则派上了用场，虽然 Java 解析 IEEE 浮点数编码的代码在网上很容易可以找到，但是前提是需要知道 C 语言对于浮点数的编码使用了 IEEE 编码，如果连这点都不知道的话，那么就连要在网上怎么找都比较难了。

今天，我来将 IEEE 二进制浮点数的表示方式进行一个简单的介绍。

浮点数

在 C 语言中，有两种存储浮点数的方式，分别是 float 和 double ，当然了还有long double。这几种浮点型所容纳的长度不同，当然它们存储的精度也就不同了。

对于整形而言，比如 int 、short 、char 之类的，在内存中的存储方式都是用 补码 进行表示。而浮点数在内存中并没有使用补码进行表示。浮点数在内存中存储的方式使用了 IEEE 的编码表示方式，即使用 符号、指数 和 尾数 的形式进行存储的。

IEEE浮点数表示

用 IEEE 编码表示浮点数，需要 3 部分进行表示，分别是 符号、指数 和 尾数。符号位占用 1 位，0 表示正数，1 表示负数。指数 和 尾数 根据 float 和 double 类型的不同而长度不同。

IEEE 二进制浮点数的表示：

位数　　符号位　　指数位　　尾数位
32　　   1       8         23 　　   单精度（float）
64　　   1       11        52 　　  双精度（double）

编码转换

以单精度为例：把 3.75 用 IEEE 表示法表示

1. 把 10 进制转换为 2 进制：

3.75D = 11.11B

2. 尾数正规化

1.111 * 2 ^ 1

3. 修正指数

1 + 127 = 128 1000 0000

4. 符号

0 表示正，1 表示负

5. IEEE表示

0 1000 0000 1110 0000 0000 0000 0000 000
(0)    (1000 0000) (1110 0000 0000 0000 0000 000)
符号位  指数        尾数 

6. 转换为16进制

0100 0000 0111 0000 0000 0000 0000 0000  
   4    0    7    0    0    0    0    0 

用 C 程序进行验证

写一个简单的 C 程序来验证上面的转换，代码如下：

#include <stdio.h>

int main()
{
    float f = 3.75f;

    printf("%f \r\n", f);

    return 0;
}

以上代码用 VS 2015 编译，调试运行查看内存，如下图所示。

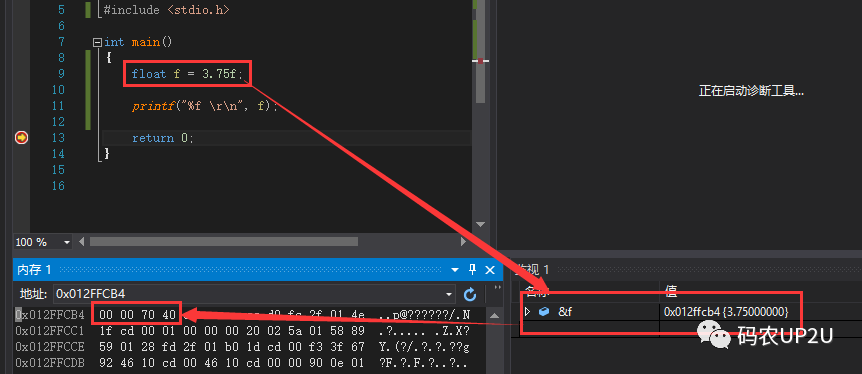
图中的 00 00 70 40 是以小尾方式存储的，其值为 40 70 00 00，与我们手动转换的值相同。关于小尾和大尾存储方式就是另外的话题了，这里就不再讨论。

关于 double 的存储方式与之类似，这里也就不进行介绍了。